Seguramente durante tus clases de estadística escuchaste hablar del Teorema de Bayes o la Regla de Bayes y sus múltiples aplicaciones. Pero, ¿aún no te queda claro? En este espacio analizaremos un ejemplo que de seguro te ayudará a entender este tema.
Veamos este ejercicio. Se sabe que una urna amarilla contiene 3 bolas negras y 1 blanca, y que una urna roja contiene 2 bolas blancas y 2 negras. Si se tira un dado, con la condición de que si el número resultante es divisible por 3, se elige la urna amarilla, y en cualquier otro caso se elige la urna roja.
De la urna elegida se saca una bola al azar. Si la bola es negra, ¿cuál es la probabilidad de que haya sido sacada de la urna amarilla?
Un diagrama de árbol nos ayudará a entender este problema.
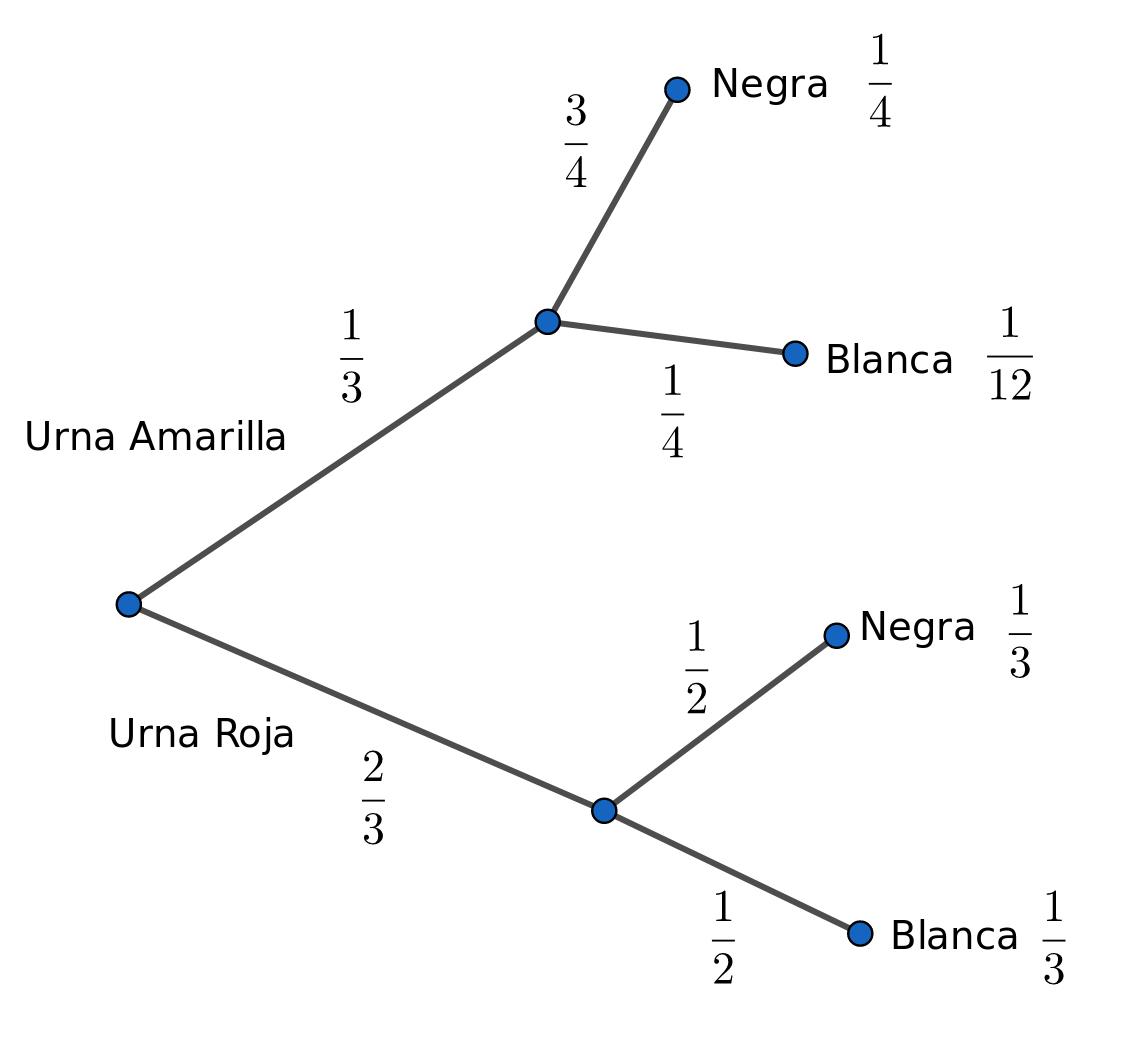
Las posibles opciones para del dado son: 1,2,3,4,5 y 6. Sólo el 3 y el 6 son divisibles por 3. Así que la probabilidad de elegir de la urna amarilla es de: 2/6=1/3, y la probabilidad de elegir de la urna roja es 4/6=2/3.
Ahora la probabilidad de escoger la urna amarilla es 1/3 y la probabilidad de sacar una bola negra, considerando que se escogió la urna amarilla es 3/4. Por tanto, la probabilidad de escoger una bola negra de la urna amarilla es: 1/3*3/4 =3/12=1/4.
De manera similar, la probabilidad de escoger la urna amarilla es 1/3 y la probabilidad de sacar una bola blanca, considerando que se escogió la urna amarilla es 1/4. Por tanto, la probabilidad de escoger una bola blanca de la urna amarilla es: 1/3*1/4=1/12.
Siguiendo este mismo razonamiento, ¿cuál es la probabilidad de sacar una bola negra de la urna roja? En efecto es 1/3. Y ¿cuál es la probabilidad de sacar una bola blanca de la urna roja? También es 1/3.
¿Suman uno las cuatro probabilidades? Es decir, ¿1/4+1/12+1/3+1/3=1? Realiza las operaciones y te darás cuenta que así es.
A partir de la fórmula de probabilidad condicional, se sabe que la probabilidad de que se seleccione la urna amarilla considerando que se sacó una bola negra es:

Sin embargo, la única manera de obtener una bola negra es:
-
sacarla de la urna amarilla o
-
sacarla de la urna roja.
Así

Por lo tanto, la probabilidad de que la bola negra haya sido sacada de la urna amarilla es:

Espero que este ejercicio te ayude a entender mejor el teorema de Bayes.
